

For non-linear functions, the rate of change of a curve varies, and the derivative of a function at a given point is the rate of change of the function, represented by the slope of the line tangent to the curve at that point.I implemented a WGS84 distance function using the average of the start and end altitude as the constant altitude. While this is beyond the scope of this calculator, aside from its basic linear use, the concept of a slope is important in differential calculus. Given the points (3,4) and (6,8) find the slope of the line, the distance between the two points, and the angle of incline: m = Given two points, it is possible to find θ using the following equation:
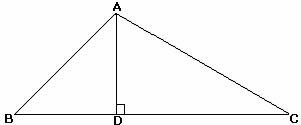
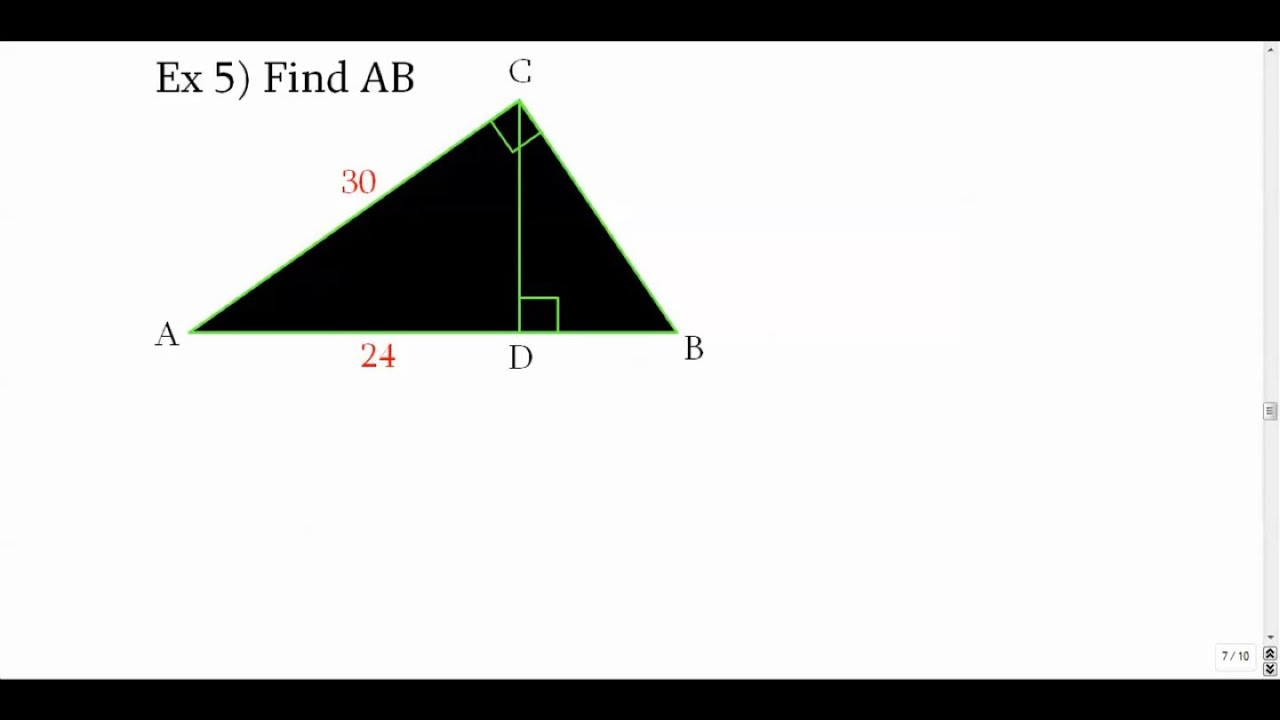
Figure 9 The altitude drawn from the vertex angle of an isosceles triangle. In Figure, the altitude drawn from the vertex angle of an isosceles triangle can be proven to be a median as well as an angle bisector. In certain triangles, though, they can be the same segments. The above equation is the Pythagorean theorem at its root, where the hypotenuse d has already been solved for, and the other two sides of the triangle are determined by subtracting the two x and y values given by two points. In general, altitudes, medians, and angle bisectors are different segments.
#Altitude geometry defintion how to
Refer to the Triangle Calculator for more detail on the Pythagorean theorem as well as how to calculate the angle of incline θ provided in the calculator above. Since Δx and Δy form a right triangle, it is possible to calculate d using the Pythagorean theorem. Recall from Definition NEUT.99(C) the definitions of altitude and base of a triangle. It can also be seen that Δx and Δy are line segments that form a right triangle with hypotenuse d, with d being the distance between the points (x 1, y 1) and (x 2, y 2). Since Age e AB, by Definition NEUT3(C) is the midpoint of AB. In the equation above, y 2 - y 1 = Δy, or vertical change, while x 2 - x 1 = Δx, or horizontal change, as shown in the graph provided. The slope is represented mathematically as: m = We discuss how Altitude geometry simple definition can help students learn Algebra in this blog post. In the case of a road, the "rise" is the change in altitude, while the "run" is the difference in distance between two fixed points, as long as the distance for the measurement is not large enough that the earth's curvature should be considered as a factor. Definition-Geometry Basics-Altitude This collection of clip art images includes image sequences for key topics in geometry. Slope is essentially the change in height over the change in horizontal distance, and is often referred to as "rise over run." It has applications in gradients in geography as well as civil engineering, such as the building of roads. Other tools include 3D by Volume (useful for pond design) and 3D By Slope to Target.
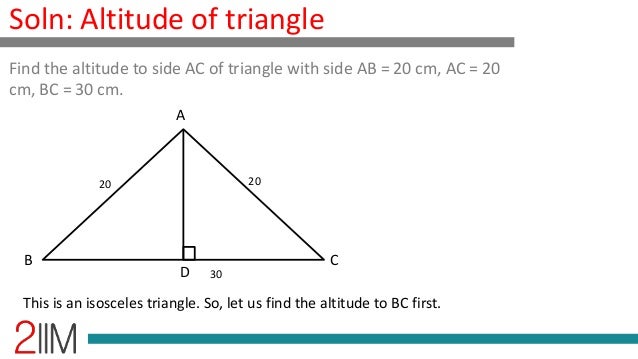
The larger the value is, the steeper the line. How to use the Leg Geometric Mean Theorem. As the picture below shows, sometimes the altitude does not directly meet the opposite side of the triangle. Generally, a line's steepness is measured by the absolute value of its slope, m. Altitude in a Triangle Definition: an altitude is a segment from the vertex of a triangle to the opposite side and it must be perpendicular to that segment (called the base). Slope, sometimes referred to as gradient in mathematics, is a number that measures the steepness and direction of a line, or a section of a line connecting two points, and is usually denoted by m. The altitude is measured as the distance from the vertex to the base and so it is also known as the height of a triangle.


 0 kommentar(er)
0 kommentar(er)
